Tries

Retrieval data structure. That’s what a Trie is known for, and that’s the easiest way to remember. A Trie is a special kind of a tree that handles string operations more conveniently. The entire English dictionary can be stored in a trie instead of a hash table. A trie is a tree-like data structure where the nodes of the tree stores the entire alphabet, and strings or words can be retrieved by traversing down a branch path of the tree. The shape and structure of a trie is always a set of linked nodes, connecting back to an empty root node. An important thing to note is that the number of child nodes in a trie depends completely upon the total number of values possible. For example, in the English alphabet, there are 26 letters, therefore, the total number of child nodes will be 26.

So what is the structure of a TrieNode? Well, looking at the cross-section of one of these nodes, there are only two things:

1. An array of references of its child nodes, all of which are null in the beginning.
2. boolean flag isEndOfWord to indicate if current node is last char of an inserted string.

class TrieNode {
public:
	TrieNode *children[ALPHA_SIZE]; // size of the alphabet is 256.
	bool isEndOfWord; // true if the node represents end of a word.
	TrieNode() : isEndOfWord(false) {
		for(int i = 0; i < ALPHA_SIZE; i++)
		children[i] = NULL; 
	}
};

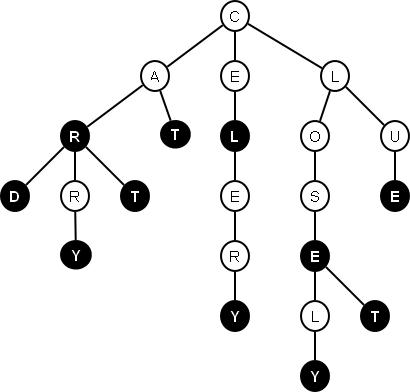
The figure below is an example of a trie filled with several english words, you notice that the black coloring refers to the isEndOfWord flag to indicate the end of the word. Looking at the farmost left branch, there are two words inserted in Trie which are “CAR” and “CARD”.

Regarding Complexities,

let W be the number of strings and L be the length of the longest string.

1. Worst case Space Complexity of creating a trie is O(W * L * ALPHABET_SIZE)
2. Worst case Time Complexity of searching/adding/deleting a string in a trie is O(L)
3. Average case Time Complexity of searching/adding/deleting a string in a trie is O(L)

Tries in C++

Tries in Go