Heaps & Priority Queues
A heap is a datastructure that stores the data in a way where the smallest/largest element can be accessed in constant time, i.e., in Big O(1).
Binary Heaps are in general implemented using an array, however, we visualize it as a complete binary tree where the value of the parent is either smaller/greater than its children, depending on the variant that you want to implement.
There are two variants of Heaps:
- Max Heap - Largest value is at the root of the tree
- Min Heap - Smallest value is at the root of the tree
Well in that case, what is the Priority Queue?
Priority Queue as a definition, it is an abstract data type (ADT) based on Heaps. You can consider that Heaps and Priority Queues are both the same thing. We define a priority queue based on whether it is a Min or a Max heap, and we use it to solve our problem.
First let’s define a Priority Queue class.
class PriorityQueue {
private:
int *A;
int capacity;
int size;
int Parent(i);
int Left(i);
int Right(i);
void HeapifyUp(int i);
void HeapifyDown(in i);
public:
PriorityQueue();
void Push(const int& e);
void Pop();
int Top();
bool IsFull();
bool IsEmpty();
~PriorityQueue();
};As mentioned earlier, a heap is just an array visualized as a complete binary tree, so whenever we want fo find parent or child of a specific index, we calculate a certain formula to get that index.
Parent(index) = (index - 1) / 2
LeftChild(index) = (index * 2) + 1
Parent(index) = (index * 2) + 2
Based on that, let’s cover the following methods that need to be implemented to preserve the order and the structure of the Heap.
Pushing an element to a Heap relies on two things:
- Insert an element at the end of the heap.
- Recursively Bubble Up the element to its correct place whether it is higher/lower than its parent.
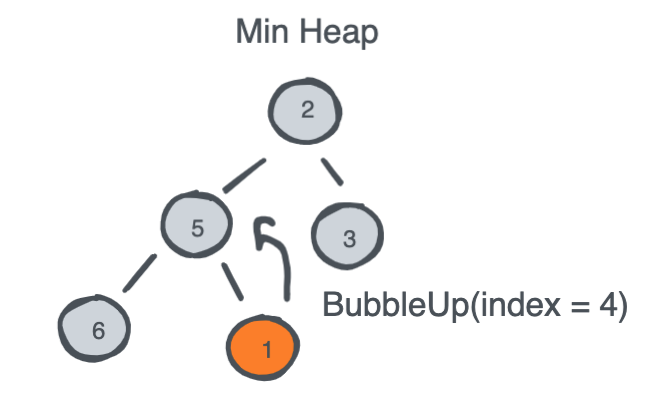
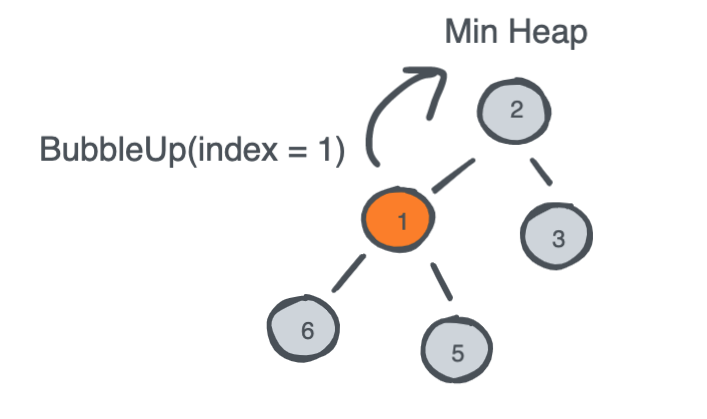
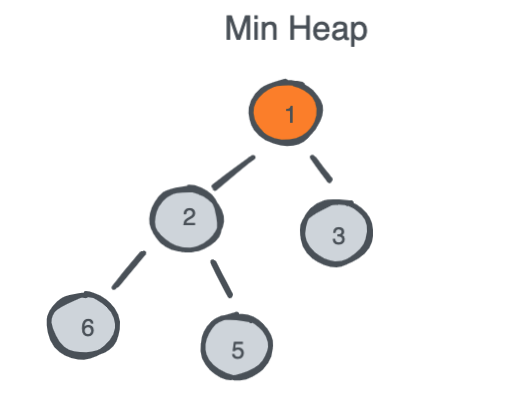
Popping an element from a Heap relies on three things:
- Swap the top element with the last element in the heap.
- remove the last element from the heap (could be as simple as decrementing the array size).
- Recursively Bubble Down the newly swapped top element to its correct place whether it is higher/lower than its children.
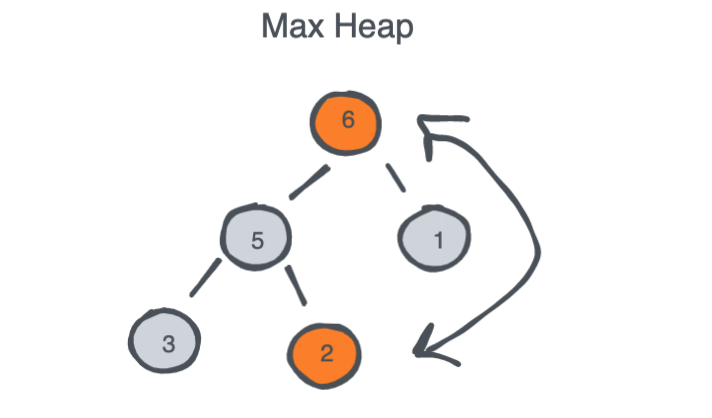
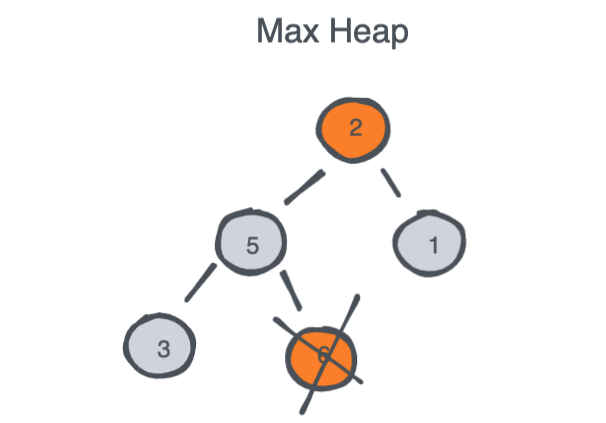
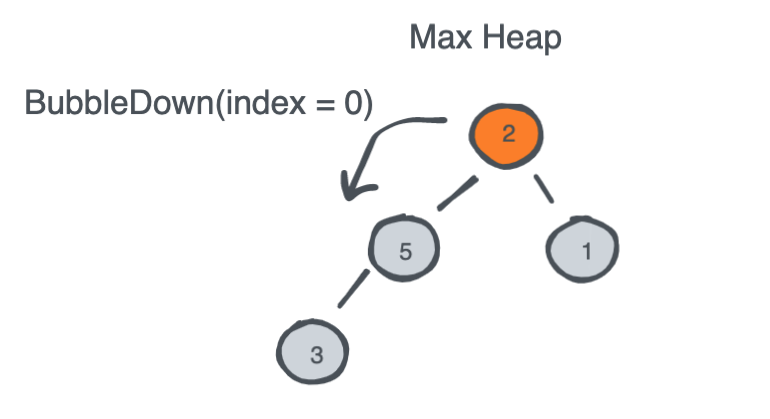
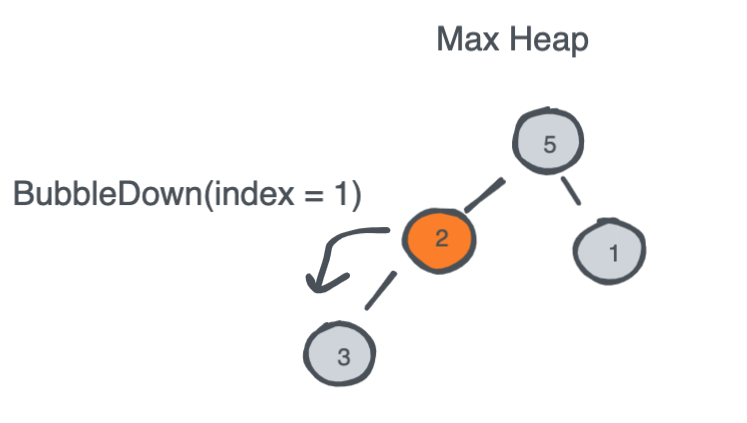
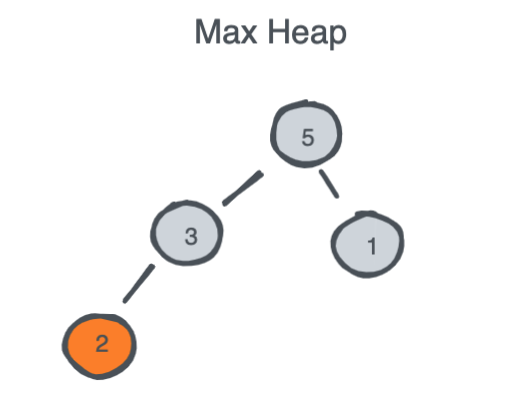
Once you implement BubbleUp() and BubbleDown() methods which are also known as HeapifyUp() and HeapifyDown(), you will use them in Push() and Pop() methods and the rest of the implementation is straight forward.
When it comes to time complexity…
| Push | O(LogN) |
| Pop | O(LogN) |
| Top | O(1) |
