Red Black Trees
Red-Black Trees! where C++ STL libraries such as set, multiset, and map are implemented using Red-Black Trees as one of many other balanced trees. So a one word to represent the core of Red Black Trees is, balance!
A Red Black Tree is not a totally new data structure, it is rather an augmented form of a very popular datastructure, Binary Search Trees! It is a Balanced Binary Search Tree that ALWAYS guarantee the dynamic set operations of time complexity O(logN) in the worst case where N is the number of nodes in the tree.
- Search(T, key)
- Insert(T, key)
- Delete(T, key)
- Successor(T, key)
- Predecessor(T, key)
- Maximum(T)
- Minimum(T)
There are 4 properties that must hold in a Red-Black Tree:-
- Every node must be colored black or red.
- Root node AND leaves are always colored black.
- For any red node, its children must be black. No red node can have a red child.
- For node x, any simple path from x to its descendent leaf must have the same number of black nodes. Also known as black height bh(x).
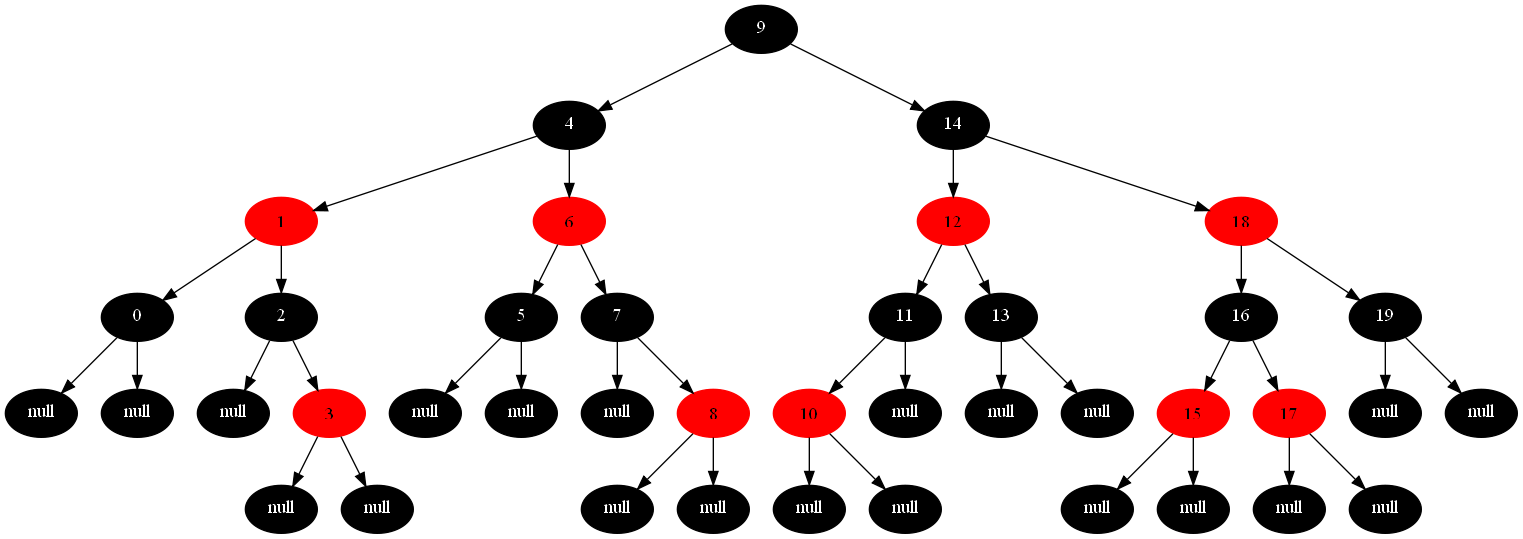
An example of a Red Black Tree.
As you can see, the node structure of a RB tree is the same as BST node structure, just augmented with an extra bit of information, its color. …
// an (RBT) Node structure.
class RedBlackNode {
public:
RedBlackNode *parent;
RedBlackNode *left;
RedBlackNode *right;
int val;
int color; // Red -> 1 | Black -> 0
RedBlackNode(int k) : val(k) {
parent = NULL;
left = NULL;
right = NULL;
color = 1;
};
};However, to ensure a logarithmic time complexity of the Red-Black Tree, each update query (Insert/Delete) is followed by another method called RB-INSERT-FIXUP and RB-DELETE-FIXUP that provides some maintenance to the tree structure to make sure the four enlisted properties are well preserved, and if there is a violation, it gets fixed. They are not super easy I have to say, but you gotta admire the amount of effort and intellect put into this data structure to handle these cases. I’ll explain the modified insertion and deletion operations in the following section. But first, Insert and then Delete operations, after rotation!
Rotation... but why?
There might be cases where the height of a branch might be larger than the height of the other branch, giving it this imbalanced shape. So by pivoting around two nodes X and Y, you can re-balance the tree!
So There are 4 cases for an imbalanced tree.
- Left Left Case (LL)
- Left Right Case (LR)
- Right Left Case (RL)
- Right Right Case (RR)
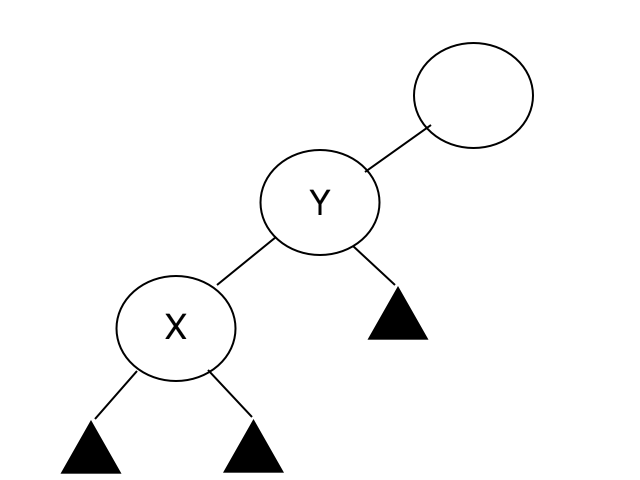
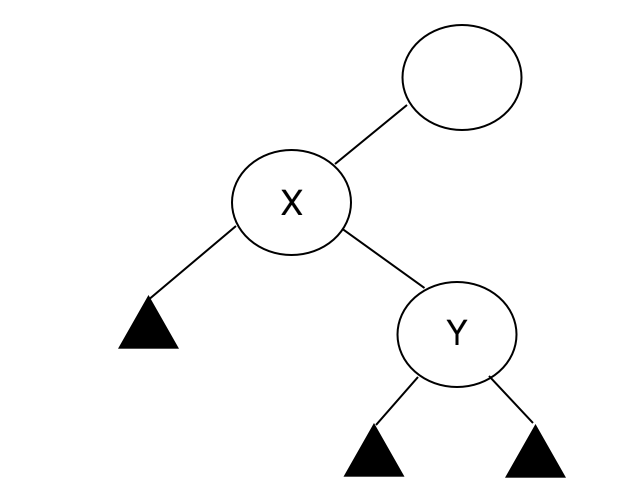
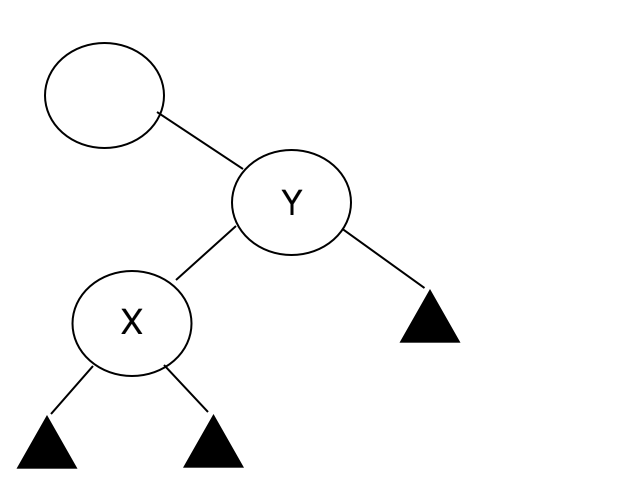
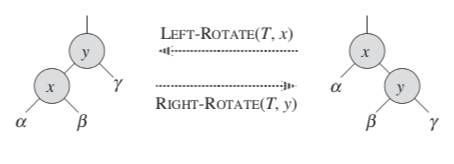
source ["CLRS, Introduction to Algorithms"]
RBT Insert
Everytime we insert a new node into our RBT, we need to do some maintenance checking to preserve the properties of the Red-Black Tree in case any violation occurs. There are two possible violations upon insertion:
- Red Violation: A red node has a red child.
- Black Violation: One path has more black nodes than another path.
There are 6 cases to handle when we insert a new node in a balanced tree, three of them are symmetric so its actually 3 cases and we handle those cases with two tools; either by changing some pointer structure (rotation) or node reconfiguration (recoloring).
RBT Delete
Deleting a node in a RBT is slightly more complicated than inserting a node in a RBT. I will not cover it in detail here, but the idea is similar to how we perform RBT Insert.
We perform a traditional BST delete + RBT FixUp, and FixUp refers to either rotation or recoloring of the nodes to preserve the properties of a RBT.
| Operation | Best Case | Average Case | Worst Case |
|---|---|---|---|
| Search | O(lgN) | O(lgN) | O(lgN) |
| Insert | O(lgN) | O(lgN) | O(lgN) |
| Delete | O(lgN) | O(lgN) | O(lgN) |
